Manuel de laboratoire pour contrôleurs embarqués

Voici un petit programme Python destiné à remplir un tableau avec des valeurs représentant les ordonnées des points d’une courbe sinusoïdale. Chacune de ces valeurs consiste en un entier non signé codé sur 8 bits (octet), variant donc théoriquement de 0 à 255 (256 valeurs), grâce à un décalage positif de 128. Ça fonctionnera donc parfaitement avec un convertisseur numérique-analogique (CNA) unipolaire 8 bits.

# Création d’une table d’onde en Python 3.3 pour un tableau de données en langage C utilisant des octets non signés
# Tableau à 256 entrées, plage d’amplitude 0-255
# Note : renommer le tableau en fonction de l’onde générée

import math

fn = input("Entrer le nom du fichier tableau à créer: ")
#Pour les utilisateurs de Python 2.x, remplacer la ligne ci-dessus par la ligne ci-dessous
#fn = raw_input("Entrer le nom du fichier tableau à créer: ")
fil = open( fn, "w+" )
fil.write( "unsigned char sinetable[256]={" )

for x in range( 256 ):

    # Chaque donnée représente 1/256ème du cycle, la valeur de crête est 127
    f = 127.0 * math.sin( 6.28319 * x / 256.0 )

    # Conversion en entier et transposition de la courbe vers des valeurs positives
    v = int( round( f, 0 ) ) + 128

    # Empêche de sortir de l’intervalle valide au cas où
    if v > 255:        
        v = 255
    if v < 0:
        v = 0

    if x < 255:
        fil.write( str(v) + ", " )
    else:
        fil.write( str(v) + "};" )

fil.close()

Pour générer ce tableau, il nous suffit d’exécuter le programme ci-dessus, d’entrer un nom de fichier valide à la demande et d’attendre une seconde l’achèvement du processus. Nous n’avons plus alors qu’à ouvrir le fichier ainsi créé dans un éditeur de texte pour copier ensuite son contenu dans l’éditeur de l’EDI Arduino. Ce programme peut être utilisé en tant que programme générique pour créer, si besoin, d’autres tables d’onde.

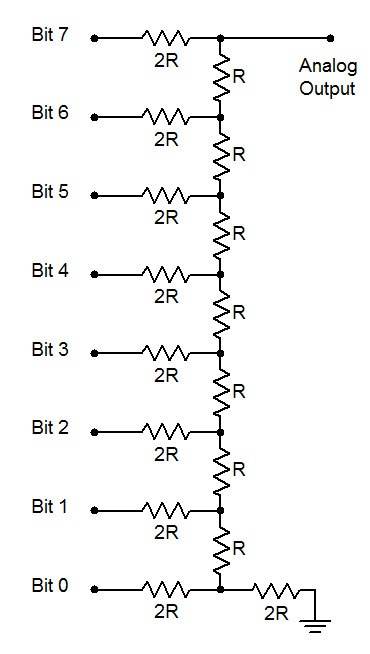
#!/usr/bin/python3

Maintenant que nous disposons des valeurs représentatives de notre onde, quel type de convertisseur numérique-analogique allons-nous utiliser ? Naturellement, nous pourrions utiliser un convertisseur du commerce, mais nous pouvons également obtenir des résultats exploitables en utilisant un simple réseau en échelle de type R-2R comme celui de la figure ci-dessous. La valeur de R pourrait se situer aux alentours de 10 kΩ, ce qui entraîne naturellement une valeur de 20 kΩ pour les résistances 2R. Bien que la tolérance des valeurs des résistances et les fluctuations de la tension de sortie entraînent un manque de linéarité de ce dispositif, les résultats obtenus sur des données codées sur 8 bits sont suffisants dans un premier temps.

Choisissez une valeur appropriée pour R et réalisez le réseau en échelle. Connectez le réseau au port D de l’Arduino comme indiqué sur la figure en faisant correspondre Bit0 avec la broche 0 (LSB) jusqu’à Bit7 avec la broche 7 (MSB). La sortie analogique devrait être analysée avec un oscilloscope. (NDLR : voir le tableau en annexeAnnexe pour les correspondances entre les broches de l’Arduino UNO et les ports de l’ATmega 328P.)

Le code destiné à générer l’onde sinusoïdale est assez simple : il est en fait très succinct. La plus grosse partie est occupée par le tableau de données. Voici la première version :

unsigned char sinetable[256]={128, 131, 134, 137, 140, 144, 147, 150, 153, 156, 159, 162, 165, 168, 171, 174, 177, 179, 182, 185, 188, 191, 193, 196, 199, 201, 204, 206, 209, 211, 213, 216, 218, 220, 222, 224, 226, 228, 230, 232, 234, 235, 237, 239, 240, 241, 243, 244, 245, 246, 248, 249, 250, 250, 251, 252, 253, 253, 254, 254, 254, 255, 255, 255, 255, 255, 255, 255, 254, 254, 254, 253, 253, 252, 251, 250, 250, 249, 248, 246, 245, 244, 243, 241, 240, 239, 237, 235, 234, 232, 230, 228, 226, 224, 222, 220, 218, 216, 213, 211, 209, 206, 204, 201, 199, 196, 193, 191, 188, 185, 182, 179, 177, 174, 171, 168, 165, 162, 159, 156, 153, 150, 147, 144, 140, 137, 134, 131, 128, 125, 122, 119, 116, 112, 109, 106, 103, 100, 97, 94, 91, 88, 85, 82, 79, 77, 74, 71, 68, 65, 63, 60, 57, 55, 52, 50, 47, 45, 43, 40, 38, 36, 34, 32, 30, 28, 26, 24, 22, 21, 19, 17, 16, 15, 13, 12, 11, 10, 8, 7, 6, 6, 5, 4, 3, 3, 2, 2, 2, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 3, 3, 4, 5, 6, 6, 7, 8, 10, 11, 12, 13, 15, 16, 17, 19, 21, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 43, 45, 47, 50, 52, 55, 57, 60, 63, 65, 68, 71, 74, 77, 79, 82, 85, 88, 91, 94, 97, 100, 103, 106, 109, 112, 116, 119, 122, 125};


void setup()
{
    // Configurer tout le port D en sortie
    DDRD = 0xff;
}
void loop()
{
    unsigned char u=0;
    unsigned char *p;

    p = sinetable;

    // Boucle indéfiniment
    while( 1 )
    {
        // Écrit la donnée et introduit l’intervalle d’échantillonnage
        PORTD = p[u++];
        delayMicroseconds(100);
    }
}

Ce code commence par configurer le port D en sortie. La fonction loop() est une boucle while() infinie. Il est intéressant de noter que cette fonction n’a pas l’occasion de boucler, dans la mesure où une fonction while() infinie également (while(1)) empêche le programme principal de continuer. Le contenu du programme principal pourrait tout aussi bien être placé dans la fonction setup(), cela fonctionnerait parfaitement. Le fait de mettre ce code dans la section loop() permet de séparer le programme proprement dit des initialisations, et est de plus cohérent avec la structure d’un sketch Arduino.

Un pointeur est défini et pointe sur le début du tableau. Ce n’est techniquement pas nécessaire ici, car nous pourrions tout aussi bien utiliser sinetable[]. La raison de ce choix va devenir évidente dans un instant. La première valeur du tableau est copiée sur le port D. Le réseau en échelle transforme la combinaison des huit tensions 0 ou 5 volts résultantes en une tension continue unique. Il est intéressant de noter l’efficacité de l’écriture « en bloc » d’une valeur sur le port D comparée à l’écriture séquentielle de la même valeur à l’aide de la fonction orientée bit digitalWrite() examinée plus tôt. Écrire les bits un par un sera source de désordre car cela entraînera la génération de sept tensions successives différentes en sortie du réseau en échelle avant d’aboutir à la bonne tension quand les huit bits seront écrits. Quoi qu’il en soit, après écriture de la valeur, le programme fait une pause de 100 µs : c’est la période d’échantillonnage. Après cette pause, la valeur suivante contenue dans le tableau est envoyée à son tour vers le port D et le processus recommence. Abstraction faite de la durée de la boucle et de celle de l’accès/écriture, le processus complet de lecture du tableau nécessite 256 processus unitaires de 100 µs soit 25,6 ms, ce qui donne une fréquence de sortie d’approximativement 39 Hz.

Saisissez le code et téléversez-le sur la carte. Connectez un oscilloscope sur la sortie analogique Analog Output du réseau R-2R. Celui-ci devrait afficher une sinusoïde d’une fréquence approximative de 39 Hz, d’une amplitude d’environ 5 volts de crête à crête, décalée de 2,5 volts. Étirez la base de temps pour analyser la courbe. Les marches d’escalier induites par le réseau en échelle devraient être visibles, ainsi que la pause de 100 µs à chaque étape.

On peut augmenter ou diminuer la fréquence en modifiant la valeur fournie à la fonction delayMicroseconds(). Essayez une valeur plus élevée pour voir ce que ça donne. 10 µs devrait générer une fréquence d’environ 390 Hz. Pour cette fréquence, mesurez le THD (taux de distorsion harmonique) résiduel de la sinusoïde. En utilisant des résistances à 5 %, le THD devrait descendre en dessous de 1 %. Une partie de cette distorsion harmonique est due à la tolérance dans la valeur des résistances ainsi qu’à des valeurs légèrement différentes de la tension de sortie présente sur chacune des broches du port D.

Différentes formes d’onde peuvent être générées et incorporées au programme, la seule modification à effectuer dans celui-ci étant au niveau de l’affectation du pointeur p, lequel devra pointer sur d’autres tableaux. Vous pourriez par exemple dupliquer le tableau actuel en modifiant son nom, disons wackysinetable[], et en modifier quelques valeurs d’une quantité suffisante pour que ce soit visible à l’oscilloscope. Pointez sur la nouvelle table en faisant p= wackysinetable; et testez le résultat. Si vous disposez d’un petit amplificateur, vous pourriez envisager de le connecter à la sortie du réseau en échelle pour écouter sur un casque le rendu de l’onde nouvellement modifiée. Vous avez devant vous des heures d’expérimentations distrayantes ! Appelez maintenant votre famille, vos amis, rameutez les voisins et lâchez les chiens : tous conviendront que c’est une meilleure façon de se distraire que de s’abrutir devant la télé.

Bien qu’il soit amusant de changer manuellement le délai (donc la période et par conséquent la fréquence), d’éditer manuellement les tableaux et d’écouter les résultats obtenus, il serait plus utile de pouvoir contrôler ces paramètres à l’aide de commandes externes, comme celles présentes sur les générateurs de fonctions standards qu’on trouve dans les laboratoires.

Comment fournir à l’utilisateur un contrôle sur la forme de l’onde ? Beaucoup de générateurs de fonctions de laboratoire disposent de barrettes de boutons-poussoirs mutuellement exclusifs, c’est-à-dire qu’un seul bouton peut être enfoncé à un moment donné : toute pression sur un autre bouton libérera le bouton précédemment enclenché. Cela offre un bon retour visuel et tactile. Une solution plus simple et moins coûteuse consiste à utiliser un unique bouton permettant de se déplacer séquentiellement parmi les choix offerts, en revenant sur le premier choix en fin de séquence. C’est très efficace quand le nombre de choix est relativement restreint. Nous pourrions coupler ce dispositif et une série de LED pour visualiser le choix effectué. En arrière-plan, une unique variable mémorisera ce choix et sera mise à jour à chaque utilisation de ce bouton. Ce bouton devrait disposer d’un dispositif anti-rebond matériel car un anti-rebond logiciel prendra trop de temps. Nous pouvons vérifier le choix en cours au début de chaque cycle. Ceci offre potentiellement deux avantages par rapport à une vérification effectuée après écriture sur le port :

• diminution des traitements à effectuer ;
• si la configuration des tableaux est correcte, nous pouvons garantir que la commutation entre deux formes d’onde aura toujours lieu lors d’une variation positive de la tension au passage du 0 volt, évitant des régimes transitoires potentiellement dangereux.

Traitons le cas avec les trois ondes suivantes : sinusoïdale, carrée et rampe. Nous aurons besoin de trois LED, une par onde, pour afficher la sélection en cours, et donc de trois broches configurées en sortie. Nous aurons de plus besoin d’une broche configurée en entrée pour le commutateur d’ondes. Bien que la variable mémorisant le choix puisse se contenter de stocker les valeurs 1, 2 ou 3, par exemple, pour représenter chacune des ondes possibles, il sera plus judicieux de s’épargner du travail en faisant coïncider ces valeurs avec les adresses des broches sur le port utilisé. De cette manière, la même variable servira à sélectionner l’onde et la LED correspondante. Nous utiliserons ici quatre des huit broches reliées au port B :

• broche 9 : port B bit 1 pour le commutateur ;
• broches 10, 11 et 12: port B bits 2, 3 et 4 pour les LED correspondant respectivement aux ondes sinusoïdale, carrée et rampe.

Nous pourrions utiliser ce qui suit :

// Tout sur le port B
#define WAVEBIT        0x02
#define SINEWAVE        0x04
#define SQUAREWAVE                0x08
#define RAMPWAVE        0x10

Nous devons alors modifier la fonction setup() comme suit :

// Configure B.2:4 en sortie
DDRB |= (SINEWAVE | SQUAREWAVE | RAMPWAVE);

// Configure B.1 en entrée, active le pull-up
DDRB &= (~WAVEBIT);
PORTB |= WAVEBIT;

Dans la fonction loop(), nous aurons besoin de nouvelles variables :

unsigned char wavechoice=SINEWAVE; 
unsigned char waveswitch=PINB & WAVEBIT, currentwaveswitch=PINB & WAVEBIT;

wavechoice est la variable qui mémorise l’onde courante choisie par l’utilisateur : elle est initialisée à SINEWAVE (onde sinusoïdale). Il est important de garder à l’esprit que nous changerons d’onde lors d’une transition (changement d’état) du bouton-poussoir et non sur son état « haut » ou « bas » en lui-même. Il est donc nécessaire de connaître son état antérieur aussi bien que son état courant. Les variables waveswitch et currentwaveswitch sont utilisées pour mémoriser ces deux états : pressé ou relâché. Plutôt que de les positionner à 1/0 (true/false), on utilisera directement la valeur actuelle du bit correspondant. Cela rendra le code un peu plus transparent. Aussi, avant d’entrer dans la boucle while(), il nous faudra positionner le pointeur de tableau sur le tableau par défaut.

// Sélectionne la sinusoïde par défaut et allume la LED correspondante à cette onde
PORTB |= wavechoice;
p = sinetable;

Comme la variable wavechoice stocke l’état des bits du port correspondant aux LED, il suffit de la copier sur le port de sortie pour synchroniser les LED (souvenez-vous que tous les autres bits sont mis par défaut à zéro lors du reset) : simple et de bon goût.

Jetons maintenant un coup d’œil sur le processus de commutation. Nous devons d’abord déterminer l’état courant :

currentwaveswitch = PINB & WAVEBIT;

La commutation n’aura lieu qu’à l’appui du bouton (c’est-à-dire lors de la transition haut/bas). Notez que si vous utilisez un circuit anti-rebond matériel inverseur, la logique devra être inversée elle aussi (supprimer le « not »).

if( !currentwaveswitch ) // Activé (bas)
{
    if( currentwaveswitch != waveswitch ) // Transition
    {

Nous vérifions alors l’état courant de la variable wavechoice et bouclons parmi les valeurs valides, en mettant à jour le pointeur de tableau par la même occasion :

        if( wavechoice == SINEWAVE )
        {
            wavechoice = SQUAREWAVE;
            p = squaretable;
        }
        else
        {
            if( wavechoice == SQUAREWAVE )
            {
                wavechoice = RAMPWAVE;
                p = ramptable;
            }
            else
            {
                wavechoice = SINEWAVE;
                p = sinetable;
            }
        }

On éteint toutes les LED et on applique le nouveau choix :

        // Éteint toutes les LED
        PORTB &= (~(SINEWAVE| SQUAREWAVE| RAMPWAVE));

        // Allume la LED sélectionnée
        PORTB |= wavechoice;
    }
}

Enfin, on met à jour la variable waveswitch afin que la logique de détection de transition fonctionne correctement :

waveswitch = currentwaveswitch;

Tout ce qui reste à faire est d’insérer cette portion de code dans une clause if() afin de n’effectuer le contrôle du commutateur qu’en début de tableau. Ceci se produit quand la variable index u est égale à zéro.

if( !u )
{
    // Gestion du commutateur d’ondes
}

Créez deux nouveaux tableaux pour les formes d’onde carrée et rampe puis ajoutez le code ci-dessus. Câblez également les trois LED ainsi que le commutateur de forme d’onde. Téléversez le sketch et testez l’utilisation à l’aide d’un oscilloscope. Le programme Python vu plus haut pourra être utilisé pour créer les nouveaux tableaux :

• le tableau de l’onde carrée contiendra 128 entrées à 255 suivies de 128 entrées à 0 ;
• le tableau de l’onde rampe contiendra 256 entrées commençant à 0 et se terminant à 255, chacune des entrées valant la précédente augmentée de 1, soit [0, 1, 2, 3, …/… , 243, 244, 255].

Permettre à l’utilisateur de changer de forme d’onde est certainement utile, mais si l’on pouvait également lui permettre de modifier la fréquence, ce serait parfait. De prime abord, il peut sembler classique d’utiliser un potentiomètre pour modifier la fréquence. Utilisé en diviseur de tension, il fournit une tension variable que l’on peut utiliser avec la fonction analogRead() dont le résultat permettra de modifier le paramètre fourni à la fonction delayMicroseconds(). Le problème qui se pose avec cette solution est le même que celui qui se posait avec le calcul en temps réel de la sinusoïde : c’est trop long. Le temps d’acquisition du convertisseur analogique-numérique n’est pas négligeable au regard de la valeur de temporisation et influera fortement sur la fréquence de l’onde créée. Par contre, le test de l’état d’un bouton-poussoir est un processus très rapide. Ajouter un second bouton-poussoir identique à celui utilisé pour changer de forme d’onde ne pose aucun problème. Chaque pression sur ce bouton incrémentera une variable globale qui sera utilisée par la fonction delayMicroseconds() comme suit :

unsigned int g_period=100; // Initialisé à 100 µs

// Écrit la donnée et introduit l’intervalle d’échantillonnage
PORTD = p[u++];
delayMicroseconds( g_period );

À chaque pression sur le commutateur de fréquence, on augmentera la temporisation comme suit :

BumpPeriod( 1 );

La fonction BumpPeriod() masque la variable globale et permet de délimiter la plage d’utilisation en bouclant une fois la limite fixée atteinte.

void BumpPeriod( char c )
{
    g_period += c;

    // Boucle sur la plage de valeurs autorisées, c peut être négatif 
    if( g_period < 1 )    g_period = 200;
    if( g_period > 200 )    g_period = 1;
}

Une temporisation de 1 µs entraîne une période de 256 µs (si on néglige la durée des processus) pour une fréquence maximale d’environ 3,9 kHz. De la même manière, une temporisation de 200 µs produira une fréquence minimale d’à peu près 20 Hz. Retenez que g_period est une variable globale et que, comme telle, elle est définie en dehors et avant toute fonction. Dans cette mesure, toutes les fonctions peuvent y avoir accès.

Ce code fonctionne et nous pourrions l’utiliser tel quel pour gérer le commutateur de fréquences, mais il pose un problème pratique. Chaque pression sur le bouton incrémentera la fréquence d’échantillonnage de seulement 1 µs. Nous disposons potentiellement d’une plage de 200 valeurs à parcourir ce qui, potentiellement, peut amener à appuyer 200 fois sur le bouton si on veut reculer d’une unité. Ce n’est probablement pas ce que souhaite faire l’utilisateur.

Une solution courante à ce type de problème réside dans l’utilisation d’un bouton à incrémentation automatique lorsqu’on maintient la pression suffisamment longtemps. Ce temps de maintien peut être de l’ordre de 500 ms. Il ne faut pas que l’incrémentation soit trop rapide, au risque de ne pas pouvoir incrémenter d’une seule unité : une période de 100 ms fera l’affaire. C’est l’équivalent de 10 pressions par seconde (ou le résultat de trop d’expressos). À cette vitesse, on parcourt la plage en 20 s juste en laissant le doigt appuyé sur le bouton. L’ergonomie peut encore être améliorée en ajoutant à côté un bouton effectuant l’opération inverse (décrémentation). Le code de ce bouton sera exactement le même, à ceci près que le paramètre fourni à la fonction BumpPeriod() sera négatif. Si la plage était plus étendue, on pourrait considérer l’ajout d’un bouton effectuant une incrémentation (ou une décrémentation) de 10 unités au lieu d’une, par exemple, afin d’approcher plus rapidement la période (donc la fréquence) souhaitée. Il suffirait pour cela de donner la valeur 10 (ou -10) au paramètre fourni à la fonction BumpPeriod(). Une autre solution, classique également, consiste à modifier le facteur d’incrémentation en fonction du temps de maintien du bouton. Par exemple, l’incrémentation pourrait être de une unité toutes les 100 ms quand le bouton est maintenu appuyé entre 0,5 et 2 secondes, puis passer à 10 unités si le maintien du bouton se prolonge au-delà des 2 secondes.

// Tout sur le port B
#define FREQBIT        0x01
#define WAVEBIT        0x02
#define SINEWAVE        0x04
#define SQUAREWAVE                0x08
#define RAMPWAVE        0x10

void BumpPeriod( char c );
unsigned int g_period=100; // Initialisée à 100 µs

void setup()
{
    // Configure tout le port D en sortie
    DDRD = 0xff;

    // Configure B.2:4 en sortie
    DDRB |= (SINEWAVE | SQUAREWAVE | RAMPWAVE);

    // Configure B.0:1 en entrée, active le pull-up
    DDRB &= (~(FREQBIT | WAVEBIT));
    PORTB |= (FREQBIT | WAVEBIT);
}

La commutation des fréquences est traitée de la même manière que celle des formes d’onde, à ceci près qu’ici nous devons en plus gérer le temps. En effet, la fonctionnalité auto-incrément nécessite de détecter les 500 ms de maintien du bouton pour démarrer puis, à partir de là, de détecter des écoulements successifs de 100 ms pour effectuer les incréments. Par conséquent, en plus des variables destinées à mémoriser l’état actuel et l’état précédent du commutateur, nous aurons besoin de variables pour mémoriser la transition, c’est-à-dire le moment de l’appui sur le bouton (transitiontime), l’instant présent (currenttime) et la consigne, c’est-à-dire la durée de maintien avant déclenchement (bumptime).

unsigned char freqswitch=PINB & FREQBIT, currentfreqswitch=PINB & FREQBIT;
unsigned long transitiontime, currenttime, bumptime=500;

Les variables « xxxtime » doivent toutes être des entiers longs non signés pour pouvoir être utilisées par la fonction millis().

Voici comment fonctionne cet algorithme :

• on récupère l’état courant du commutateur : on ne fait rien tant que le commutateur n’est pas à l’état « bas » ;
• quand il est à l’état bas, on mémorise l’instant présent et on regarde si son état antérieur était l’état « haut » ;
• si oui, il s’agit d’une transition : on mémorise alors le moment de cette transition et on incrémente la période ;
• on en profite pour initialiser la consigne (bumptime) avec la valeur de maintien souhaitée (500 ms) avant le démarrage de l’auto-incrémentation.

// Vérifie si le commutateur de fréquence est activé
currentfreqswitch = PINB & FREQBIT;    

if( !currentfreqswitch ) // Activé (bas)
{
    currenttime = millis();
    if( currentfreqswitch != freqswitch ) // Transition
    {
        transitiontime = currenttime;
        BumpPeriod( 1 );
        bumptime = 500;    // Nombre de millisecondes  avant une autoincrémentation
    }

Si les états du commutateur (précédent et courant) sont les mêmes, c’est que le commutateur est maintenu dans son état courant. Avant de commencer l’incrémentation automatique, il faut savoir si la durée de ce maintien a respecté la consigne (bumptime, ou 500 ms). En soustrayant le moment de la transition de l’instant courant, nous saurons combien de temps le bouton est resté pressé. Si ce temps est au moins égal à la consigne, on peut incrémenter la période. Comme il ne faut pas réincrémenter la période pendant les prochaines 100 ms, il faudra également incrémenter la consigne (bumptime) de 100 ms.

    else    // Si maintenu, la durée de maintien est-elle suffisante?
    {
        if( currenttime-transitiontime > bumptime )
        {
            BumpPeriod( 1 );
            bumptime += 100;
        }
    }
}

Enfin, et quel que soit l’état du commutateur, on met à jour la variable stockant l’état antérieur du commutateur (freqswitch) avec la valeur contenue dans la variable stockant son état actuel (currentfreqswitch) pour détecter une nouvelle transition.

freqswitch = currentfreqswitch;

Notez qu’une fois le bouton relâché, il est ignoré jusqu’à sa prochaine utilisation. À ce moment-là, une nouvelle transition sera détectée et la consigne (bumptime) sera réinitialisée à 500 ms afin que le processus puisse se répéter comme décrit ci-dessus. Si le bouton est relâché avant que la consigne ne soit atteinte, aucune auto-incrémentation n’aura lieu, et la pression suivante sur le bouton réinitialisera la transition et la consigne.

Comme pour la commutation des formes d’onde, il est important de noter que si vous utilisez un circuit anti-rebond matériel inverseur, le « switch selected » logique sera également inversé (supprimez le « not »).

Le code du processus de commutation de fréquence doit être placé au même endroit que celui concernant le processus de commutation de forme d’onde (dans le même bloc), soit immédiatement avant, soit immédiatement après. Cette partie de la fonction loop() devrait donner quelque chose comme :

    // Sélectionne la sinusoïde par défaut et allume la LED correspondante à cette onde

    while( 1 )
    {
        // Ne vérifie l’état du commutateur qu’au début de chaque cycle 
        if( !u )
        {
            // Gestion du commutateur d’ondes
            // Gestion du commutateur de fréquences
        }

        // Écrit la donnée et introduit l’intervalle d’échantillonnage
        PORTD = p[u++];
        delayMicroseconds( g_period );
    }
}

Saisissez et téléversez ce code puis testez-le. Si vous vous en sentez le courage, vous pouvez de la même manière implémenter un bouton de décrémentations.

// Tout sur le port B
#define FREQBIT     0x01
#define WAVEBIT     0x02
#define SINEWAVE    0x04
#define SQUAREWAVE  0x08
#define RAMPWAVE    0x10

void BumpPeriod( char c );

unsigned char sinetable[256]={128, 131, 134, 137, 140, 144, 147, 150, 153, 156, 159, 162, 165, 168, 171, 174, 177, 179, 182, 185, 188, 191, 193, 196, 199, 201, 204, 206, 209, 211, 213, 216, 218, 220, 222, 224, 226, 228, 230, 232, 234, 235, 237, 239, 240, 241, 243, 244, 245, 246, 248, 249, 250, 250, 251, 252, 253, 253, 254, 254, 254, 255, 255, 255, 255, 255, 255, 255, 254, 254, 254, 253, 253, 252, 251, 250, 250, 249, 248, 246, 245, 244, 243, 241, 240, 239, 237, 235, 234, 232, 230, 228, 226, 224, 222, 220, 218, 216, 213, 211, 209, 206, 204, 201, 199, 196, 193, 191, 188, 185, 182, 179, 177, 174, 171, 168, 165, 162, 159, 156, 153, 150, 147, 144, 140, 137, 134, 131, 128, 125, 122, 119, 116, 112, 109, 106, 103, 100, 97, 94, 91, 88, 85, 82, 79, 77, 74, 71, 68, 65, 63, 60, 57, 55, 52, 50, 47, 45, 43, 40, 38, 36, 34, 32, 30, 28, 26, 24, 22, 21, 19, 17, 16, 15, 13, 12, 11, 10, 8, 7, 6, 6, 5, 4, 3, 3, 2, 2, 2, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 3, 3, 4, 5, 6, 6, 7, 8, 10, 11, 12, 13, 15, 16, 17, 19, 21, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 43, 45, 47, 50, 52, 55, 57, 60, 63, 65, 68, 71, 74, 77, 79, 82, 85, 88, 91, 94, 97, 100, 103, 106, 109, 112, 116, 119, 122, 125};
unsigned char squaretable[256]={0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255};
unsigned char ramptable[256]={0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 150, 151, 152, 153, 154, 155, 156, 157, 158, 159, 160, 161, 162, 163, 164, 165, 166, 167, 168, 169, 170, 171, 172, 173, 174, 175, 176, 177, 178, 179, 180, 181, 182, 183, 184, 185, 186, 187, 188, 189, 190, 191, 192, 193, 194, 195, 196, 197, 198, 199, 200, 201, 202, 203, 204, 205, 206, 207, 208, 209, 210, 211, 212, 213, 214, 215, 216, 217, 218, 219, 220, 221, 222, 223, 224, 225, 226, 227, 228, 229, 230, 231, 232, 233, 234, 235, 236, 237, 238, 239, 240, 241, 242, 243, 244, 245, 246, 247, 248, 249, 250, 251, 252, 253,  255};
unsigned int g_period=100; // Initialisé à 100 µs

void setup()
{
  // Configure B.2:4 en sortie
  DDRB |= (SINEWAVE | SQUAREWAVE | RAMPWAVE);
  // Configure B.0:1 en entrée, active le pull-up
  DDRB &= (~(FREQBIT | WAVEBIT));
  PORTB |= (FREQBIT | WAVEBIT);
  // Configure tout le port D en sortie
  DDRD = 0xff; 
}

void loop()
{
  unsigned char u=0;
  unsigned char *p;
  unsigned char wavechoice=SINEWAVE; 
  unsigned char waveswitch=PINB & WAVEBIT, currentwaveswitch=PINB & WAVEBIT;  
  unsigned int g_period=100; // Initialisé à 100 µs
  unsigned char freqswitch=PINB & FREQBIT, currentfreqswitch=PINB & FREQBIT;
  unsigned long transitiontime, currenttime, bumptime=500;  
  // Sélectionne la sinusoïde par défaut et allume la LED correspondante à cette onde
  PORTB |= wavechoice;
  p = sinetable;
  // Boucle indéfiniment
  while( 1 )
  {
    if( !u )
    {  
      currentwaveswitch = PINB & WAVEBIT;
      if( !currentwaveswitch ) // Activé (bas)
      {
        if( currentwaveswitch != waveswitch ) // Transition
        {
          if( wavechoice == SINEWAVE )
          {
            wavechoice = SQUAREWAVE;
            p = squaretable;
          }
          else
          {
            if( wavechoice == SQUAREWAVE )
            {
              wavechoice = RAMPWAVE;
              p = ramptable;
            }
            else
            {
              wavechoice = SINEWAVE;
              p = sinetable;
            }
          }
          // Éteint toutes les LED
          PORTB &= (~(SINEWAVE| SQUAREWAVE| RAMPWAVE));

          // Allume la LED sélectionnée
          PORTB |= wavechoice;
        }
      }
      waveswitch = currentwaveswitch;
      // Vérifie si le commutateur de fréquence est activé
      currentfreqswitch = PINB & FREQBIT;  
      if( !currentfreqswitch ) // Activé (bas)
      {
        currenttime = millis();
        if( currentfreqswitch != freqswitch ) // Transition
        {
          transitiontime = currenttime;
          BumpPeriod( 1 );
          bumptime = 500; // Nombre de millisecondes  avant une autoincrémentation
        }
        else  // Si maintenu, la durée de maintien est-elle suffisante?
        {
          if( currenttime-transitiontime > bumptime )
          {
            BumpPeriod( 1 );
            bumptime += 100;
          }
        }
      }  
      freqswitch = currentfreqswitch;
    }   
    // Écrit la donnée et introduit l’intervalle d’échantillonnage
    PORTD = p[u++];
    delayMicroseconds( g_period );
  }

} // Fin de void Loop()

void BumpPeriod( char c )
{
  g_period += c;

  // Boucle sur la plage de valeurs autorisées, c peut être négatif 
  if( g_period < 1 )  g_period = 200;
  if( g_period > 200 )  g_period = 1;
}

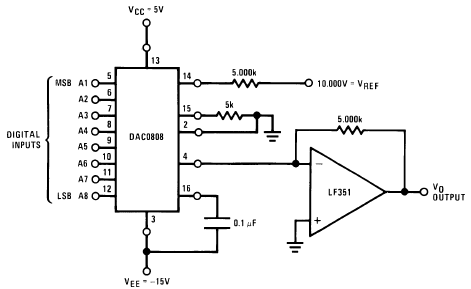
Si le réseau en échelle R-2R est tout à fait utilisable pour cette application, on ne peut certainement pas dire qu’il soit très précis. Si une résolution supérieure en bits est souhaitée, l’accumulation d’erreurs dues à l’imprécision des résistances et des tensions pourrait rendre le bit de poids faible LSB non significatif. De plus, pour un fonctionnement correct, le réseau R-2R ne doit pas être trop sollicité. Il serait intéressant de rendre la sortie insensible à une sollicitation importante et d’augmenter la précision du système. Ce but peut être atteint par une modification raisonnable du câblage, avec l’utilisation d’un simple convertisseur numérique-analogique (CNA) à entrée parallèle 8 bits, alimentant un buffer de sortie à amplificateur opérationnel. Un bon exemple de ce produit est le DAC0808 de Texas Instrument dont vous pouvez télécharger la fiche technique ici.

Le DAC8080 est un convertisseur numérique-analogique (CNA, DAC en anglais) à entrées parallèles 8 bits, dont la sortie est modulée en courant (intensité). Son utilisation nécessite un minimum de composants externes. Les huit broches de sortie du microcontrôleur sont connectées directement aux huit broches d’entrée du CNA (en ce qui nous concerne, la totalité du réseau R-2R peut être supprimée). Comme le CNA utilise une sortie modulée en courant, il est naturel d’utiliser un amplificateur opérationnel en mode conversion courant/tension (source de tension contrôlée en courant) pour fournir une tension de sortie stable. Un bon exemple est proposé dans la fiche technique sous la référence « Typical application » (voir figure ci‑dessous).

L’amplificateur opérationnel LF351 peut être remplacé par le circuit LF411 plus récent. Notez également que l’alimentation du circuit est absente du schéma et qu’un condensateur de couplage peut être requis en sortie pour compenser un éventuel décalage de tension. Câblez cette variante et testez-la. Portez la fréquence à 390 Hz avec une onde sinusoïdale et mesurez le THD résiduel. Comparez-le avec celui mesuré précédemment avec le réseau R-2R.

En imaginant qu’un bouton de décrémentation ait été ajouté à cette réalisation, la totalité des ports B et D est utilisée sur l’Arduino UNO, et il ne reste que six broches disponibles, les broches analogiques (de A0 à A5). Si d’autres ports étaient disponibles, l’affichage de la fréquence en cours pourrait être une option intéressante. Cela peut être réalisé avec sept broches supplémentaires (ou huit si le point décimal est requis) pour piloter les sept segments d’un afficheur, auxquelles s’ajouteront trois ou quatre broches (en fonction de la précision désirée pour l’affichage de la fréquence) destinées à réaliser le multiplexage. Plusieurs cartes de la famille Arduino, comme la carte Arduino MEGA, sont capables de gérer ça.

La technique utilisée ici pour changer la fréquence est connue sous le nom de « fréquence d’échantillonnage variable ». Elle est relativement simple mais offre quelques inconvénients, dont le moindre n’est pas la difficulté à filtrer la sortie (processus destiné à supprimer le phénomène « marches d’escalier » affectant l’onde, dont on n’a pas parlé).

Une autre technique consiste à utiliser une fréquence d’échantillonnage élevée et constante. La fréquence est modifiée lors de la génération de l’onde désirée par interpolation dans un tableau plus grand. La charge de calcul est un peu plus élevée, mais même une simple interpolation linéaire peut aboutir à un résultat de grande qualité sans beaucoup de temps de traitement supplémentaire.

Pour finir, ce type d’application peut bénéficier de l’utilisation d’interruptions temporisées. Elles peuvent être vues comme des bribes de code s’exécutant à des intervalles de temps bien définis, contrôlés dans ce cas par les timers/counters embarqués. Le timer sera utilisé pour déclencher une interruption logicielle, afin d’éviter d’avoir recours à la fonction bloquante delayMicroseconds(). La routine d’interruption n’aura guère d’autre objet que de copier la valeur suivante du tableau sur le port de sortie. Cette technique permettra la génération d’une onde régulière et libérera la fonction loop() pour scruter l’état des commutateurs et effectuer les gestions associées.

Correspondances Arduino-ATmega 328P

Les deux programmes Python 3 pour générer les tables d’ondes « carrée et rampe » :

#!/usr/bin/python3

# Création de la table d'ondes carrées, 256 entrées,
# amplitude variant de 0 à 255.


fn = input("Entrez le nom du fichier table d'onde à créer: ")
fil = open( fn, "w+" )

fil.write( "unsigned char squaretable[256]={" )

for x in range(128):
  fil.write('0, ')
for x in range(127):  
  fil.write('255, ')
fil.write('255};')

fil.close()

#!/usr/bin/python3

# Création de la table d'ondes en rampe, 256 entrées,
# amplitude variant de 0 à 255.


fn = input("Entrez le nom du fichier table d'onde à créer: ")
fil = open( fn, "w+" )

fil.write( "unsigned char ramptable[256]={" )

for x in range(254):
  fil.write(str(x) + ", ")
fil.write("255};") 

fil.close()