Manuel de laboratoire pour contrôleurs embarqués

Utilisation du langage C et de la plateforme Arduino

VI. Les boucles▲

Dans cet exercice, on s'attardera sur l'utilisation des boucles ou comment itérer. Quelques fonctions utiles dans la bibliothèque standard seront étudiées. Les ordinateurs sont évidemment idéals pour les calculs répétitifs comme ceux nécessaires pour remplir des tables de données.

Si un nombre d'itérations précis est requis, une construction avec la boucle for est généralement le meilleur choix. Dans les situations où le nombre d'itérations n'est pas connu à l'avance, ou quand la condition de fin de boucle peut être exprimée de façon plus aisée, la boucle while() est préférable. Cet exercice se limitera à utiliser les constructions avec la boucle while(), bien qu'une fois le code saisi, vous seriez tenté de le modifier au profit d'une boucle for().

Ce programme servira à produire une table de valeurs concernant des circuits RC en série (NDLR circuits analogiques du 1^er ordre permettant la réalisation de filtres passe-bas). Il calculera et affichera les valeurs qui pourront servir à tracer un diagramme de Bode. Ce diagramme montre le gain ou l'atténuation en sortie d'un circuit en réponse à la fréquence. Dans cet exemple, la tension aux bornes du condensateur sera prise comme grandeur de sortie. On utilise plus couramment le gain en décibel (ou dB) au lieu du gain absolu calculé à partir du rapport des tensions. Ce programme ne permettra pas de tracer la courbe, mais plutôt de produire les coordonnées des points de la courbe pour que vous puissiez la tracer vous-même.

Premièrement, le programme aura besoin d'obtenir les valeurs de résistance et capacité de la part de l'utilisateur. Avec ces valeurs, il calculera et affichera la fréquence de coupure, f_c. L'utilisateur devra alors saisir la plage de fréquences pour le calcul des gains. Il lui sera demandé de donner une fréquence de départ, une fréquence de fin et le nombre de points de fréquence à calculer par décade (une décade correspond à un facteur 10 entre deux nombres).

Habituellement, l'échelle linéaire sur l'axe des abscisses (l'axe des fréquences) n'est pas privilégiée, et on lui préfère une représentation sur une échelle logarithmique. Avec cette nouvelle échelle, deux graduations dont le rapport vaut une valeur donnée sont à distance constante. Par exemple, si la plage du tracé est entre 100 Hz et 1000 Hz et que l'on veut deux points par décade, on ne retiendra pas les valeurs 100, 550 et 1000 (1000 débutant une nouvelle décade, 100 et 550 sont alors considérés comme les « deux points par décade »).

550 est à égale distance de 100 et 1000, mais le rapport 550/100=5,5 est plus grand avec la graduation de départ, qu'avec la graduation de fin, car 1000/550≈1,82. En fait, on retiendra les graduations 100, 316 et 1000, car les rapports 316/100 et 1000/316 sont égaux tous les deux à 3,16. Simple, non ! Réfléchissez à la spécification « deux points par décade ». On veut un nombre qui lorsqu'il est multiplié par lui-même vaut 10, c'est-à-dire égal à la racine carrée de 10 (3,16). Si on veut cinq points par décade, on utilisera la racine cinquième de 10, et ainsi de suite.

Note de la rédaction

550 est à mi-distance entre 100 et 1000, car 550-100=1000-550=450. Sur une échelle logarithmique, le milieu géométrique entre les graduations 100 et 1000 est à la graduation 316, car log(316)-log(100)=log(316/100) est égal à log(1000)-log(316)=log(1000/316).

Voici un pseudo-code pour commencer :

Donner des indications à l'utilisateur ;
Obtenir de l'utilisateur les valeurs de la résistance en ohms et de la capacité en farads ;
Calculer et afficher la fréquence de coupure ;
Obtenir de l'utilisateur les fréquences de départ et de fin (en Hz) ainsi que le nombre de points par décade ;
Afficher l'en-tête de la table, c'est-à-dire fréquence (Hz) et gain (dB) ;
Déterminer le facteur multiplicateur de la fréquence à partir du nombre de points par décade ;
Initialiser la fréquence à la valeur de départ ;
Commencer à boucler sur la fréquence tant qu'elle est inférieure à la fréquence de fin ;
Calcul du gain en dB ;
Afficher la fréquence et la valeur du gain correspondant ;
Multiplier la fréquence par le facteur calculé au 6. pour obtenir la valeur suivante de la fréquence ;
Fin de la boucle, puis fin du programme.

La seule chose qui pourrait rester un peu floue est le calcul du gain et sa conversion en décibels (dB). La conversion en décibels est définie par la formule suivante :

kitxmlcodelatexdvpdb=20\times\log _{10}\left(gain\right)finkitxmlcodelatexdvp

En gros, le gain s'obtient grâce à un diviseur de tension réalisé entre la résistance et la réactance capacitive. Ainsi, on peut détailler l'étape 9 :

9a. Déterminer la réactance capacitive X_C.

9b. Calculer le gain basé sur le diviseur de tension : kitxmlcodeinlinelatexdvp\frac{-jX_C}{R-jX_C}finkitxmlcodeinlinelatexdvp, (Rappel : le module de l'expression est kitxmlcodeinlinelatexdvp\frac{X_C}{\sqrt{R^2+{X_C}^2}}finkitxmlcodeinlinelatexdvp).

9c. Calculer le gain en dB avec la formule : kitxmlcodeinlinelatexdvpdb=20\times\log _{10}\left(gain\right)finkitxmlcodeinlinelatexdvp.

La bibliothèque de fonctions mathématiques (math.h) nous sera très utile pour les fonctions usuelles comme les logarithmes, racines carrées et autres. Les fonctions qui nous concernent ici sont : pow(), log10() et sqrt().

Le programme

Premièrement, remarquez l'utilisation de #define pour le nombre pi et les définitions de prototypes de fonctions. Les fonctions, bien que de petites tailles, rendent le programme principal beaucoup plus lisible.

Sélectionnez

#include <stdio.h>
#include <math.h>

#define M_PI 3.141592653

void give_directions( void );
double find_fc( double res, double cap );
double find_xc( double freq, double cap );
double find_dB( double gain );

int main( void )
{
  double r, c, xc, gain, dB, steps;
  double fc, f, fstart, fstop, ffactor;
  give_directions();
  printf("Entrez la resistance en ohms :");
  scanf("%lf", &r);
  printf("Entrez la capacite en Farads :");
  scanf("%lf", &c);
  fc = find_fc( r, c );
  printf("\nLa frequence de coupure est %lf Hertz.\n\n", fc);
  printf("Entrez la frequence de depart en Hertz :");
  scanf("%lf", &fstart);
  printf("Entrez la frequence de fin en Herz :");
  scanf("%lf", &fstop);
  printf("Entrez le nombre de pas a afficher par decade :");
  scanf("%lf", &steps);
  printf("Frequence (Hz)\t\t\tGain (dB)\n"); /* \t is a tab */
  ffactor = pow( 10.0, 1.0/steps );
  f = fstart;
  while( f <= fstop )
  {
    xc = find_xc( f, c );
    gain = xc/sqrt(r*r + xc*xc); /* On pourrait utiliser pow() ici pour elever au carre, mais la multiplication du nombre par lui-meme s'execute plus rapidement */
    dB = find_dB( gain );
    printf("%10.1lf\t\t%10.1lf\n", f, dB ); /* %10.1lf 10 espaces avec 1 chiffre apres la virgule */
    f *= ffactor; /* raccourci pour f=f*ffactor; */
  }
}

void give_directions( void )
{
  printf("Generation tableau de Bode\n\n");
  printf("Ce programme affichera les gains en dB pour un circuit RC serie\n");
}

double find_fc( double res, double cap )
{
  return( 1.0/(2.0*M_PI*res*cap) );
}

double find_xc( double freq, double cap )
{
  return( 1.0/(2.0*M_PI*freq*cap) );
}

double find_dB( double gain )
{
  return( 20.0 * log10( gain ) );
}

Saisissez ce programme et testez-le pour différents couples de valeurs en entrée. Examinez ce qui pourrait mal tourner avec ce programme, et comment vous pourriez contourner les problèmes. Par exemple, considérez ce qui pourrait arriver si l'utilisateur saisissait une valeur nulle pour la résistance, ou si la fréquence de fin était plus petite que la fréquence de départ.

Note de la rédaction
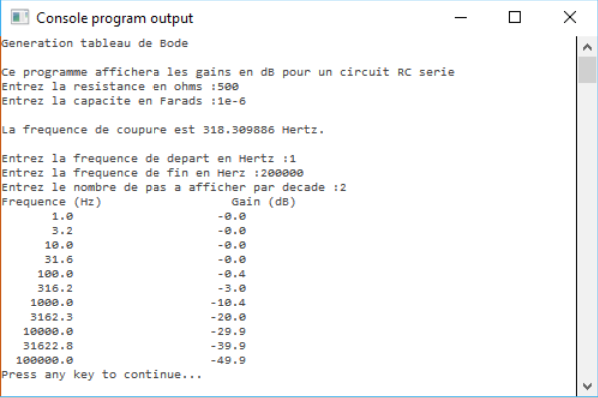
Exemple de sortie console obtenue dans l'EDI Pelles C :

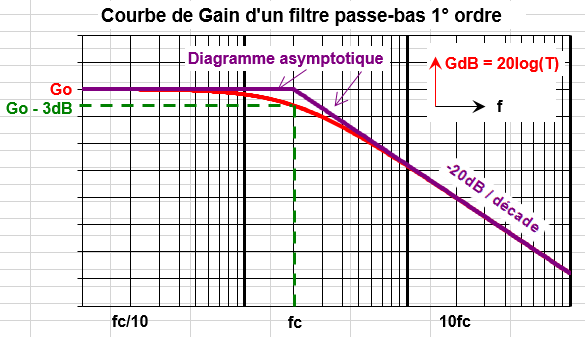
À la fréquence de coupure, le gain est de -3 dB.
Remarquez que pour des fréquences élevées, la courbe tend asymptotiquement vers une droite de pente -20 dB par décade. Et l'on retrouve les résultats classiques du filtre passe-bas du 1^er ordre de la figure ci-dessous.

Aménagements et évolutions

Il y a deux évolutions possibles de ce programme une fois que vous aurez complété cet exercice. La première, déjà mentionnée plus tôt, consiste à aménager la boucle en passant par une construction avec une boucle for(). La deuxième consiste à rajouter une troisième colonne pour le calcul de la phase pour chaque valeur de fréquence. En effet, un diagramme de Bode complet comporte deux courbes, une pour le gain en fonction de la fréquence, et l'autre pour la phase en fonction de la fréquence.